Calculator scavenger hunt

Before using any calculator, I think there are basic aspects to be aware of:

1. Does the calculator preserve order of operations? Give your test input and result. Was the result mathematically correct?
2. How does the calculator handle division by zero?
   • Fractions (e.g., \( \frac{2}{0} \), \( 0^0 \))
   • Graph a curve with a removable discontinuity (i.e., a "hole"). Give the equation of the curve tested.
   • Graph a vertical asymptote. Give the equation of the curve tested.
     (How to turn TI vertical asymptotes on/off)

Scavenger hunt

Describe how use your calculator to do the following:

1. Adjust the contrast of the screen.
2. Find the maximum value of \( y = x^3 + 3x^2 - 2 \) on the interval \( [-4, -1] \) two different ways without tracing.
3. Find the roots of \( y = x^3 + 3x^2 - 2 \).
4. Graph \( y_1 = x^2 \) with a dotted line and \( y_2 = x^2 - 5 \) with a continuous line.
5. "Turn off" \( y_2 \), but still keep it in memory.
6. Turn on Plot 1: StatsPlot → Enter → Enter. Now graph \( y_1 \).
7. Find the greatest common factor and least common multiple of 2136 and 4872.
8. Multiply \( (4+3i)(2-5i) \), where \( i=\sqrt{-1} \).
9. Find the real part of \( \dfrac{1}{2 + 3i}, \) expressed in fractional form. Give the calculator commands used.
10. Find the slope of the tangent line of \( y = x^3 + 3x^2 - 2 \) at \( x=2 \), two different ways.
11. Graph the following piecewise function, \( f(x) = \begin{cases} x^2, & x \le 0 \\ -x, & x > 0 \end{cases} \).
12. Create a program called HW that displays "Hello World!". (see Instructables for help)
13. Stop a graph mid graphing (useful for graphs that are taking forever). Try it on the graph \( y = nDeriv(x^2, x, x) \)
14. Find something on the calculator that looks interesting that you do NOT know what it does.

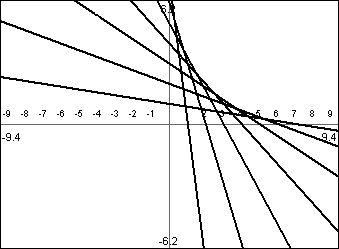
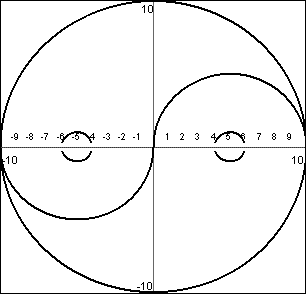
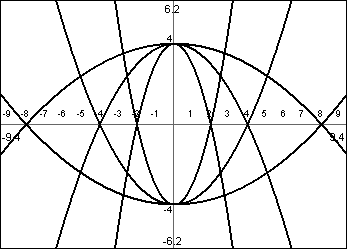
Make these designs

Provide the equations needed to make these designs.

Submission

Not required. This task is for class discussion.